BlogPower SystemInductance of Transmission lin...
Inductance of transmission line solved problems
Q) Calculate the loop inductance per km of a single-phase overhead line consisting of two conductors each 1 cm diameter and 1.2 m apart.
Given- Diameter = 1 cm; D = 1.2 m
r =0.5 *10^{-2} m
r’ = 0.003894 m
L=4\times { 10 }^{ -7 }\ln { \dfrac { D }{ r’ } }
L=2.2922\times { 10 }^{ -6 } H/m
L=2.2922\times { 10 }^{ -3 } H/km
Q) Find the loop inductance and reactance per kilometer of single-phase overhead line consisting of two conductors, each 1.213 cm diameter. The spacing between conductors is 1.25 meters and the frequency is 50 Hertz.
Given- Diameter=1.1213 cm; r=0.6065 cm = 0.6065 \times { 10 }^{ -2 } m; D=1.25 m
r’=0.7788\times0.6065 \times { 10 }^{ -2 }=0.4723 { 10 }^{ -2 } m
L=4\times { 10 }^{ -7 }\ln { \dfrac { D }{ r’ } }
L=22.31 \times { 10 }^{ -7 } H/m
L=22.31 \times { 10 }^{ -4 } H/km
X=2\pi fL=2\pi 50 \times 22.31 \times { 10 }^{ -4 } = 0.7 \Omega/km
Q) A wire 4 mm in diameter is suspended at a constant height 10 m above sea level which constitutes the return conductor. Calculate the inductance of the system per km.
Given- Diameter = 4 mm; Height= 10 m \; above \; sea \; level
r = 2 \times { 10 }^{ -3 } m
r’ = 0.7788 \times 2 \times { 10 }^{ -3 } = 0.001557 m
L=2\times { 10 }^{ -7 }\ln { \dfrac { D }{ r’ } } = 18.92 \times { 10 }^{ -7 } H/m
Note: In the above numerical the return conductor is sea therefore by using ‘method of images’ we will assume the same conductor below the sea level with a depth equal to the height of the actual conductor which is above the sea level.
Q) Calculate the loop inductance per kilometer of single-phase line comprising of two parallel conductors one meter apart and 1 cm in diameter when the material of conductor is 1) Copper 2) Steel with relative permeability 50.
Given- Diameter = 1 m; D =1 m; \mu_r (for \; steel) = 50
r=0.5 cm
r’=0.7788\times 0.5 \times { 10 }^{ -2 } = 3.894 \times { 10 }^{ -3 } m
Copper
L=4\times { 10 }^{ -7 }\ln { \dfrac { D }{ r’ } } = 2.2193 \times { 10 }^{ -6 } = 2.2193 \times { 10 }^{ -3 } H/km
Steel
L=\left[ { \mu }_{ r }+4\times \ln { \dfrac { D }{ r } } \right] { 10 }^{ -7 } =71.19 \times { 10 }^{ -7 } H/m
Note: In the above numerical observe the formula used to calculate the inductance of steel. The radius used in the above formula is actual radius r and not fictitious radius r’.
Q) A 3-phase 50 km long single circuit 66 kV transposed overhead line has horizontal spacing with 3 m between adjacent conductors and 6 m between outer conductors. The conductor diameter is 2 cm. Find the Inductance per phase.

Given- l=50km;
D=3m between adjacent conductor;
D=6m between outer conductor;
Diameter = 2 cm.
r’ = 0.7788 \times 1 \times { 10 }^{ -2 } m = 7.788 \times { 10 }^{ -3 } m
\sqrt [ 3 ]{ { d }_{ 12 }{ d }_{ 23 }{ d }_{ 31 } } =3.779663
L=2\times { 10 }^{ -7 }\ln { \dfrac { \sqrt [ 3 ]{ { d }_{ 12 }{ d }_{ 23 }{ d }_{ 31 } } }{ r’ } }
L=1.236 \times { 10 }^{ -6 } H/m
L=1.236 \times { 10 }^{ -3 } H/km
{ L }_{ 50 }=1.236\times { 10 }^{ -3 }\times 50=0.06184 H
Q) A 3-phase single circuit bundled conductor line with two sub-conductors per phase has horizontal spacing with 6.1 m between the center lines of adjacent phases. The distance between the sub conductors of each phase is 30.5 cm and each sub-conductor has a diameter of 2.54 cm. Find the inductance per phase per km.

Given- Horizontal spacing = 6.1 m;
Spacing between sub-conductors = 30.5 cm;
Diameter =2.54 cm.
r=1.27 \times { 10 }^{ -2 } m
r’= 0.7788\times 1.27 \times { 10 }^{ -2 } = 9.89076 \times { 10 }^{ -3 } m
GMR=\sqrt [ 4 ]{ r’r'{ d }_{ 1{ 1 }^{ ‘ } }{ d }_{ { 1 }^{ ‘ }1 } } =\sqrt { r'{ d }_{ 1{ 1 }^{ ‘ } } } =0.05492
\sqrt [ 3 ]{ { d }_{ 12 }{ d }_{ 23 }{ d }_{ 31 } } =7.685518
L=2\times { 10 }^{ -7 }\ln { \dfrac { \sqrt [ 3 ]{ { d }_{ 12 }{ d }_{ 23 }{ d }_{ 31 } } }{ GMR } }
= 9.8824 \times { 10 }^{ -7 } H/m
=9.8824 \times { 10 }^{ -4 } H/km
Q) A 3-phase single circuit bundled conductor line with three sub-conductors per phase has horizontal spacing with 6.1 m between the center lines of adjacent phases. The distance between the sub conductors of each phase is 30.5 cm and each sub-conductor has a diameter of 2.54 cm. Find the inductance per phase per km.
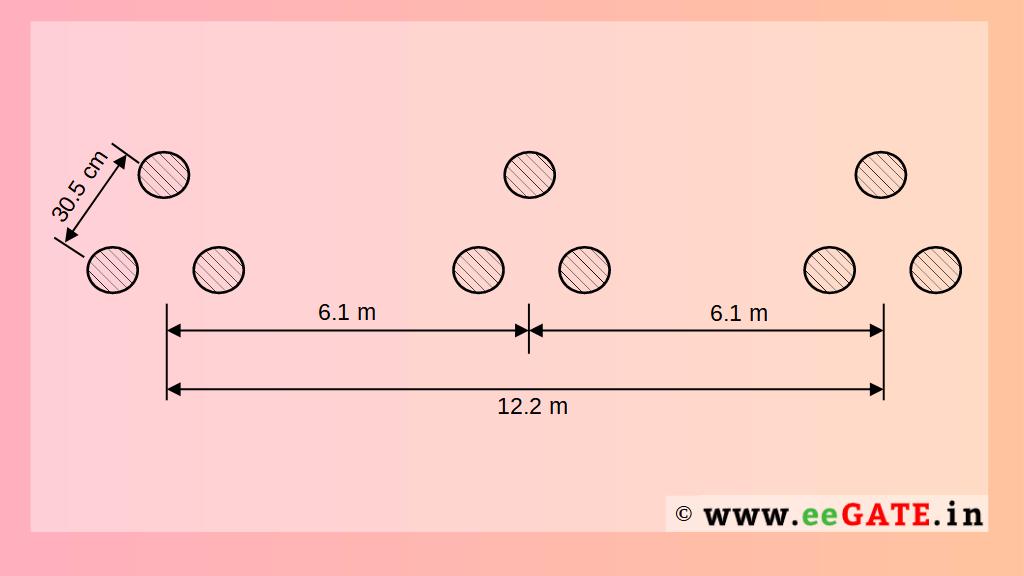
Given- Horizontal spacing = 6.1 m;
Spacing between sub-conductors = 30.5 cm;
Diameter =2.54 cm.
GMR=\sqrt [ 9 ]{ (r'{ { d }^{ 2 }) }^{ 3 } } =\sqrt [ 3 ]{ (r'{ { d }^{ 2 }) } } =0.09726
L=2\times { 10 }^{ -7 }\ln { \dfrac { \sqrt [ 3 ]{ { d }_{ 12 }{ d }_{ 23 }{ d }_{ 31 } } }{ GMR } }
L=8.7394 \times { 10 }^{ -7 } H/m
L= 8.7394 \times { 10 }^{ -4 } H/km
Q) A 3-phase double circuit line has its conductors at the vertices of a regular hexagon with a side of 3.5 m. The diameter of each conductor is 2 cm. Find the inductance per phase per km.

Given- D=3.5 m; Diameter = 2 cm
r=1 \times { 10 }^{ -2 } m
r’=0.7788 \times 1 \times { 10 }^{ -2 } = 7.788 \times { 10 }^{ -3 } m
L ={ 10 }^{ -7 } \ln { \dfrac { \sqrt { 3 } D }{ 2r’ } } = 5.964 \times { 10 }^{ -7 } H/m = 0.5964 \times { 10 }^{ -3 } H/km
Q) A double circuit 3-phase overhead line has a configuration as shown in fig. The distance between conductors a and c’ is 7.5 m, between b and b’ is 10 m and between a and c is 8 m. The radius of each conductor is 1.284 cm. Find the inductance per phase per km.
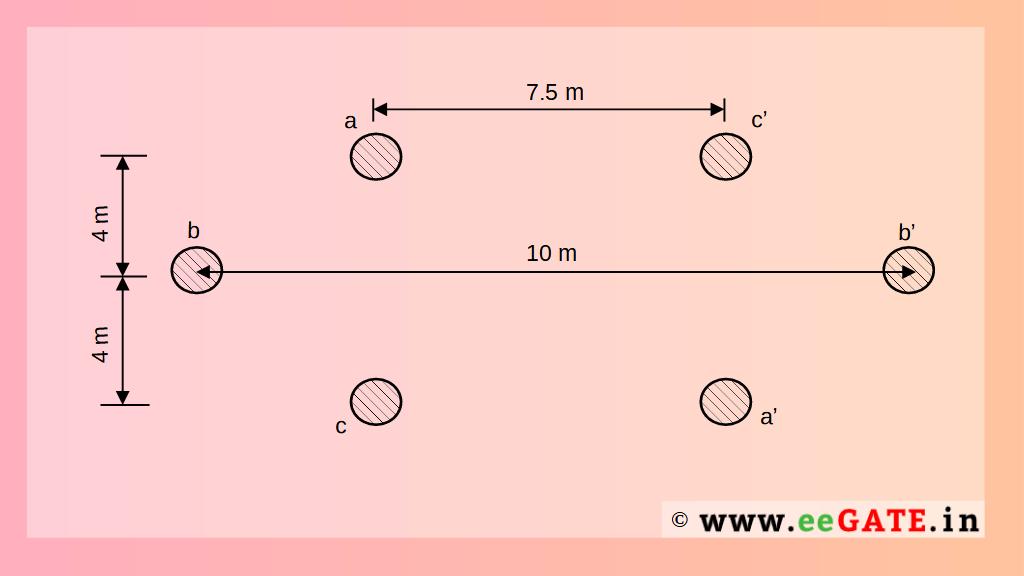
Given- r=1.284 cm =1.284 \times { 10 }^{ -2 } m
r’ = 0.7788 \times 1.284 \times { 10 }^{ -2 } = 0.009999 m
According \; to \; pythagoras \; theorem –

Distance \; between \; a \; and \; a’ \; (d_{aa’}) \; and
Distance \; between \; c \; and \; c’ \; (d_{cc’}) \; = \sqrt { { 8 }^{ 2 }+{ 7.5 }^{ 2 } } = 10.96585 m
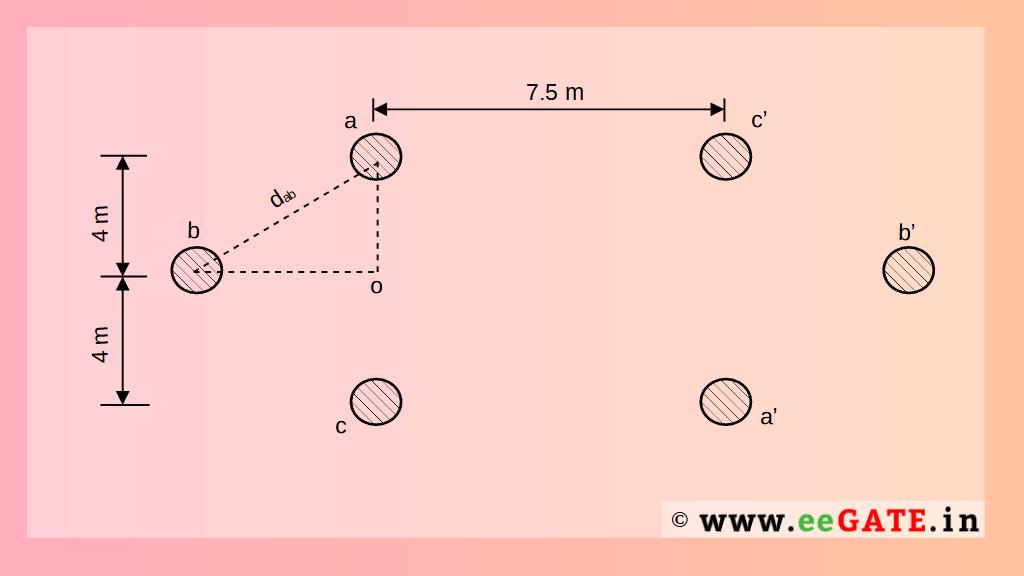
Distance \; between \; a \; and \; b \; (D_{ab}) \; and
Distance \; between \; c \; and \; b \; (D_{cb}) \; = \sqrt { { 1.25 }^{ 2 }+{ 4 }^{ 2 } } =4.1907 m

Distance \; between \; a \; and \; b’ \; (D_{ab’}) \; = \sqrt { { (7.5+1.25) }^{ 2 }+{ 4 }^{ 2 } } =9.6209 m
GMR_a = \sqrt [ 4 ]{ { (r'{ d }_{ aa’ }) }^{ 2 } } =\sqrt { r'{ d }_{ aa’ } } =0.33113 m
GMR_b = \sqrt [ 4 ]{ { (r'{ d }_{ bb’ }) }^{ 2 } } =\sqrt { r'{ d }_{ bb’ } } =0.3162 m
GMR_c = \sqrt [ 4 ]{ { (r'{ d }_{ cc’ }) }^{ 2 } } =\sqrt { r'{ d }_{ cc’ } } =0.33113 m
Total \; GMR \; (D_s) = \sqrt [ 3 ]{ 0.33113\times 0.3162\times 0.33113 } = 0.3260 m
GMD_{ab} = \sqrt [ 4 ]{ { d }_{ ab }{ d }_{ ab’ }{ d }_{ a’b }{ d }_{ a’b’ } } =\sqrt { { d }_{ ab }{ d }_{ ab’ } } =6.3491 m
Similarly,
GMD_{bc} = \sqrt { { d }_{ bc }{ d }_{ bc’ } } =6.3491 m
GMD_{ca} = \sqrt { { d }_{ ca }{ d }_{ ca’ } } =7.7459 m
{ D }_{ eq }=\sqrt [ 3 ]{ 6.3491\times 6.3491\times 7.7459 } = 6.7842 m
L=2\times { 10 }^{ -7 }\ln { \dfrac { D_{eq} }{ D_s } } = 6.07 \times { 10 }^{ -7 } H/m = 0.607 \times { 10 }^{ -3 } H/km
Q) A 3-phase line has an equilateral spacing of 6 m. It is desired to rebuild the line with same D_{eq} and horizontal configuration so that the central conductor is midway between the outers. Find the spacing between the outer conductor and central conductor.
Given- Equilateral spacing is 6m that is D_{eq} is 6 m.
Let D be the spacing between conductors when they are arranged in horizontal configuration.
Note: D_{eq} for both the configuration is same.
Note: We can take distance from center of one bundled conductor to center of other bundled conductor to calculate GMD.
D_{eq} \; for \; horizontal \; spacing = 6 =\sqrt [ 3 ]{ DD(2D) }
D = 4.7622 m
Q) The double circuit three-phase line has the configuration shown in figure the distance between conductor a and c’ is 7.5 between b and b’ is 9 m and between a and c is 8 m. Find inductance per kilometer per phase. The radius of each conductor is 1.25 cm.
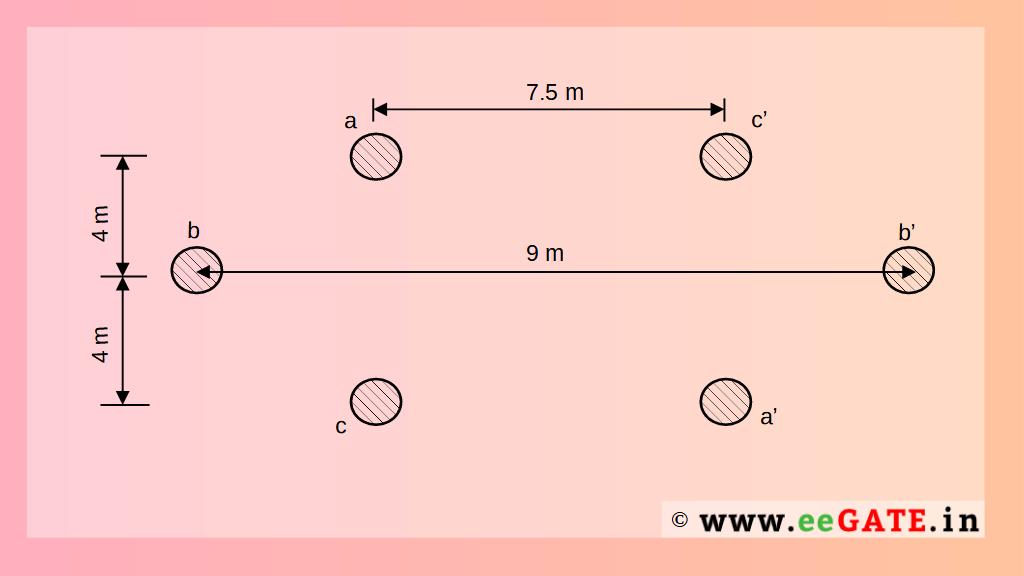
Given- r=1.25 cm =1.25 \times { 10 }^{ -2 } m
r’ = 0.7788 \times 1.25 \times { 10 }^{ -2 } = 9.735 \times { 10 }^{ -3 } m
According \; to \; pythagoras \; theorem –
Distance \; between \; a \; and \; a’ \; (d_{aa’}) \; and
Distance \; between \; c \; and \; c’ \; (d_{cc’}) = \sqrt { { (7.5+0.75) }^{ 2 }+{ 8 }^{ 2 } } = 10.9658 m
Distance \; between \; a \; and \; b \; (D_{ab}) \; and
Distance \; between \; c \; and \; b \; (D_{cb}) = \sqrt { { 0.75 }^{ 2 }+{ 4 }^{ 2 } } =4.0697 m
Distance \; between \; a \; and \; b’ \; (D_{ab’}) = \sqrt { { (7.5+0.75) }^{ 2 }+{ 4 }^{ 2 } } =9.1685 m
GMR_a = \sqrt [ 4 ]{ { (r'{ d }_{ aa’ }) }^{ 2 } } =\sqrt { r'{ d }_{ aa’ } } =0.3267 m
GMR_b = \sqrt [ 4 ]{ { (r'{ d }_{ bb’ }) }^{ 2 } } =\sqrt { r'{ d }_{ bb’ } } =0.2959 m
GMR_c = \sqrt [ 4 ]{ { (r'{ d }_{ cc’ }) }^{ 2 } } =\sqrt { r'{ d }_{ cc’ } } =0.3267 m
Total \; GMR (D_s)= \sqrt [ 3 ]{ 0.3267\times 0.3267\times 0.2959 } = 0.3160 m
GMD_{ab} = \sqrt [ 4 ]{ { d }_{ ab }{ d }_{ ab’ }{ d }_{ a’b }{ d }_{ a’b’ } } =\sqrt { { d }_{ ab }{ d }_{ ab’ } } =6.1084 m
Similarly,
GMD_{bc} = \sqrt { { d }_{ bc }{ d }_{ bc’ } } =6.1084 m
GMD_{ca} = \sqrt { { d }_{ ca }{ d }_{ ca’ } } =7.7459 m
{ D }_{ eq }=\sqrt [ 3 ]{ 6.1084\times 6.1084\times 7.7459 } = 6.61163 m
L=2\times { 10 }^{ -7 }\ln { \dfrac { D_{eq} }{ D_s } } = 6.0816 \times { 10 }^{ -7 } H/m = 0.60816 \times { 10 }^{ -3 } H/km
Q) A 765 kV single circuit line has three sub conductors per phase. Each sub conductor has a diameter of 31.68 mm and sub conductor spacing of 45 cm. The interface spacing is 15.25 m. The configuration is horizontal. Find the inductance per phase per kilometer.
Given- Spacing \; between \; sub-conductors = 45 cm = 45 \times { 10 }^{ -2 }
Spacing \; between \; conductors = 15.25 m; Diameter= 31.68 mm
r = 15.84 mm = 15.84 \times { 10 }^{ -3 } m
r’ = 0.7788 \times 15.84 \times { 10 }^{ -3 } = 0.01233 m
GMR(D_s)=\sqrt [ 3 ]{ r'{ d }^{ 2 } } =0.13566 m
GMD(D_{eq}) = \sqrt [ 3 ]{ 15.25\times 15.25\times 30.50 } =19.237 m
L=2\times { 10 }^{ -7 }\ln { \dfrac { D_{eq} }{ D_s } } = 9.9064 \times 10^{-7} H/m = 0.99064 \times 10^{-3} H/km


The final exponent in the last equation should be -3, not 3.