KVL problems with solutions
Kirchhoff’s Voltage law: The algebraic sum of all the voltages in any mesh (closed circuit) is zero.
Determination of signs while solving problems-
- Voltage Source: A positive sign is assigned to the EMF when going from the negative terminal of the voltage source to the positive terminal since there is an increase in potential. On the other hand, when moving from the positive terminal to the negative terminal, potential drops and the EMF is marked as negative.
2. Resistance: The potential drop is negative when passing through the resistance in the same direction as the current flow because the potential decreases. However, if the resistance is traversed in the opposite direction to the current flow, the potential increases, resulting in a positive voltage drop.
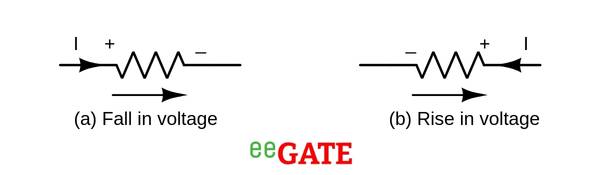
Note:
- Consider the second polarity of the voltage source / battery and resistance in the direction of current while solving the problems.
- To simplify calculations, it is advisable to always assume that the current is flowing clockwise.
1) Find the current flowing through 1 Ω resistance by using Kirchhoff’s voltage law / Mesh analysis.
For Mesh 1
130-0.2I_1-0.2I_1+0.2I_2-110=0
-0.4I_1+0.2I_2=-20 \ldots\ldots (1)
For Mesh 2
-I_2+110-0.2I_2+0.2I_1-0.2I_2=0
0.2I_1-1.4I_2=-110 \ldots\ldots (2)
I_1 = 96.1538 A (clockwise)
I_2 = 92.3076 A (clockwise)
\therefore current flowing through 1 Ω resistor is 92.3076 A (clockwise).
2) By using Kirchhoff’s voltage law (KVL) / Mesh analysis find the current flowing through a 5 Ω resistor.
For Mesh 1
2-0.1I_1-10I_1-5I_1+5I_2=0
-15.1I_1+5I_2=-2 \ldots\ldots (1)
For Mesh 2
-0.2I_2-4-5I_2+5I_1-20I_2=0
5I_1-25.2I_2=4 \ldots\ldots (2)
I_1 = 0.0855 A (clockwise)
I_2 = -0.1417 A (clockwise)
Current flowing through 5 Ω resistor is I_1-I_2 = 0.0855-(-0.1417) = 0.2272 A (clockwise)
3) By using Kirchhoff’s voltage law (KVL) / Mesh analysis find the current flowing through all resistances.
For Mesh 1
12.5-I_1-2I_1-3(I_1-I_2)=0
-6I_1+3I_2=-12.5 \ldots\ldots (1)
For Mesh 2
-2.5I_2-3I_2-3(I_2-I_1)=0
3I_1-8.5I_2=0 \ldots\ldots (2)
I_1=2.5297 A (clockwise)
I_2= 0.8928 A (clockwise)
\therefore current flowing through 1 Ω resistor is 2.5297 A (clockwise)
\therefore current flowing through 2.5 Ω resistor is 0.8928 A (clockwise)
\therefore current flowing though 2 Ω resistor is 2.5297 A (clockwise)
\therefore current flowing through 3 Ω resistor is 0.8928 A (clockwise)
\therefore current flowing through 3 Ω (middle) resistor is I_1-I_2 = 2.5297-0.8928=1.6369 A (clockwise)
4) By using Kirchhoff’s voltage law (KVL) / Mesh analysis find the current flowing through a 1 Ω resistor.
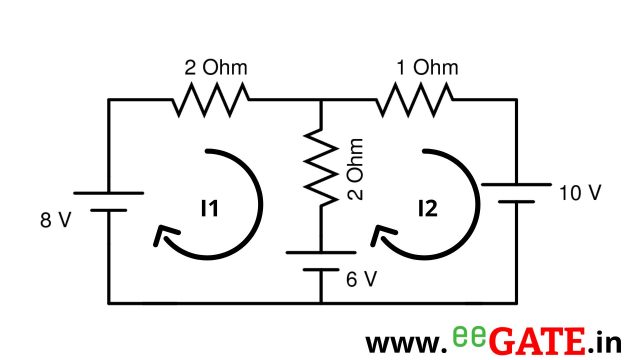
For Mesh 1
8-2I_1-2(I_1-I_2)-6=0
-4I_1+2I_2=-2 \ldots\ldots (1)
For Mesh 2
-I_2-10+6-2(I_2-I_1)=0
2I_1-3I_2=4 \ldots\ldots (2)
I_1 = -0.25 A (clockwise)
I_2 = -1.5 A (clockwise)
\therefore current flowing through 2 Ω resistor is I_1 – I_2 = -0.25-(-1.5) = 1.25 A (clockwise)
5) By using Kirchhoff’s voltage law (KVL) / Mesh analysis find the current flowing through a 4 Ω resistor.
For Mesh 1:
12-2I_1-12(I_1-I_2)-(I_1-I_3)=0
-15I_1+12I_2+I_3=-12 \ldots\ldots (1)
For Mesh 2:
-10-3(I_2-I_3)-12(I_2-I_1)-2I_2=0
12I_1-17I_2+3I_3=10 \ldots\ldots (2)
For Mesh 3:
24-(I_3-I_1)-3(I_3-I_2)-4I_3=0
I_1+3I_2-8I_3=-24 \ldots\ldots (3)
I_1 = 2.7198 A (clockwise)
I_2 = 2.05722 A (clockwise)
I_3 = 4.1114 A (clockwise)
\therefore current flowing through 4 Ω resistor is I_3 = 4.1114 A (clockwise)
6) By using KVL find Current flowing through 10 Ω resistance.
For Mesh 1
4-5I_1-15(I_1-I_2)=0
-20I_1+15I_2=-4 \ldots\ldots (1)
For Mesh 2
-10I_2-8(I_2-I_3)-15(I_2-I_1)=0
15I_1-32I_2+8I_3=0 \ldots\ldots (2)
For Mesh 3
-12I_3-6-8(I_3-I_2)=0
8I_2-20I_3=6 \ldots\ldots (3)
I_1 =0.2256 A (clockwise)
I_2 = 0.0341 A (clockwise)
I_3 = -0.2863 A (clockwise)
\therefore I_{10Ω} = 0.0341 A (clockwise)
7) Find current flowing through all resistors.
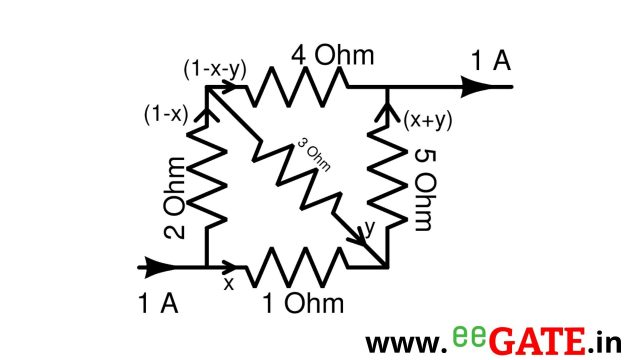
For Mesh 1:
-2(1-x)-3y+x=0
3x-3y=2 \ldots\ldots (1)
For Mesh 2:
3y-4(1-x-y)+5(x+y)=0
9x+12y=4 \ldots\ldots (2)
x= 0.5714 A
y= -0.0952 A
I_{1\Omega} = x=0.5714 A
I_{2\Omega} = (1-x)=1-0.5714 = 0.4286 A
I_{3\Omega} = 0.0952 A
I_{4\Omega} = (1-x-y) = 1-05714-(-0.0952)=0.5238 A
I_{5\Omega} = x+y = 0.5714 +(-0.0952) = 0.4762 A
8) Find potential difference between X and Y.
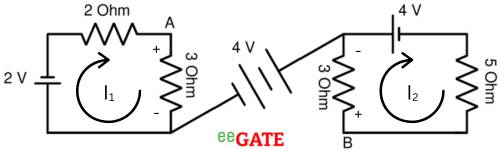
For Mesh 1-
-2-2I_1-3I_1=0
-5I_1=2
I_1 = -0.4 A
For Mesh 2-
-4-5I_2-3I_2=0
-8I_2=4
I_2 = -0.5 A
KVL equation for path X to Y.
-3I_1+4+3I_2=V_{xy}
-3*(-0.4)+4+3*(-0.5)=V_{xy}
V_{xy} = 3.7 V
9) Find potentential difference V_{XY} for given network.
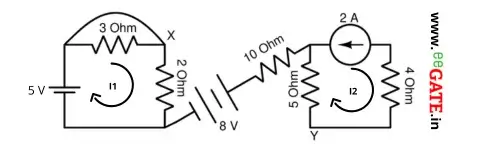
For Mesh 1 –
5 – 2I_1 = 0
I_1 = 2.5 A
For Mesh 2 –
I_2 = -2 A
For Path X to Y
V_x -2I_1+8+5I_2 – V_y = 0
V_x – V_y = V_{xy} = 7 V
Note:
- The 3 Ohm and 10 Ohm resistors are unnecessary because no current passes through them.
For theory you can refer NPTEL videos
Good 😊😊😊😊
this page really cleared all my doubts regarding KVL by providing different kinds of examples. Appreciate that!