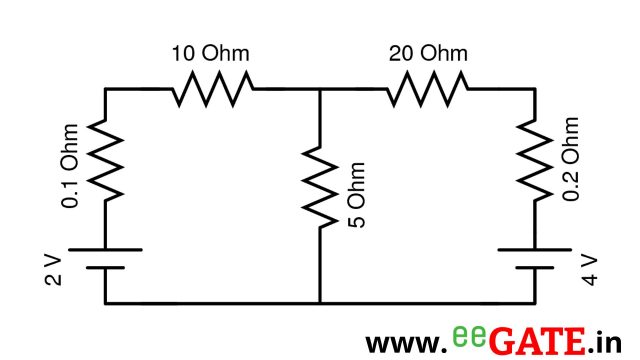
1) Find current flowing through 1 \Omega resistor.
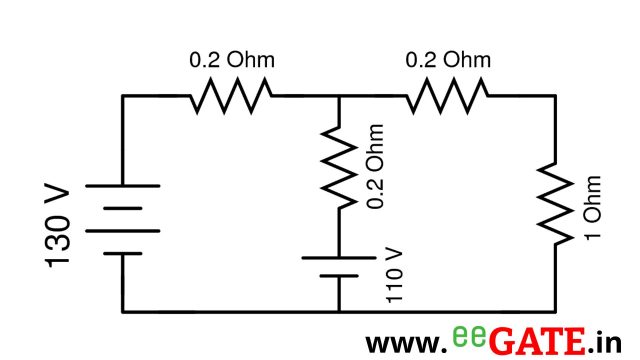
Calculate V_{th}
130-0.2I-0.2I-110 = 0
-0.4I = -20
I = 50 A
-V_{th} + 110 +0.2I = 0
V_{th} = 120 V
Calculate R_{th}
0.2 || 0.2 = 0.1 \Omega
0.1 + 0.2 = 0.3 \Omega
R_{th} = 0.3 \Omega
Thevenin’s equivalent circuit.
I_{1\Omega} = \dfrac{V_{th}}{R_{th} + R_L} = \dfrac{120}{0.3+1} = 92.3076 A
1) Find Current flowing through 1 \Omega resistor by using superposition theorem.
Consider 130 V Voltage source only.
-0.2I_1-0.2(I_1-I_2)+130 = 0
-0.4I_1 +0.2I_2 = -130 \ldots\ldots (1)
-I_1-0.2(I_2-I_1)-0.2I_2=0
0.2I_1-1.4I_2=0 \ldots\ldots (2)
I_1 = 350 A
I_2 = 50 A
I’_{1\Omega} = 50 A (\downarrow)
Consider 110 V only.
-0.2I_1 -0.2(I_1-I_2)-110 = 0
-0.4I_1+0.2I_2 = 110 \ldots\ldots(3)
-I_2+110-0.2(I_2-I_1)-0.2I_2=0
0.2I_1 – 1.4I_2 = -110 \ldots\ldots (4)
I_1 = -253.8467 A
I_2 = 42.3076 A
I’’_{1\Omega} = 42.3076 A (\downarrow)
\therefore I_{1\Omega} = I’_{1\Omega} + I’’_{1\Omega} = 50 + 42.3076 = 92.3076 A (\downarrow)
2) Find current flowing through 5 \Omega .
2-0.1I_1-10I_1-5(I_1-I_2)=0
15.1I_1 + 5I_2=-2 \ldots\ldots (1)
-20I_1-0.2I_2-5(I_2-I_1)=0
5I_1-25.2I_2=0 \ldots\ldots (2)
I_1 = 0.1417 A
I_2 = 0.02812 A
I’_{5\Omega} = I_1-I_2 = 0.1158 A (\downarrow)
Consider 4 V only.
-0.1I_1-10I_1-5(I_1-I_2) = 0
-15.1I_1+5I_2 = 0 \ldots\ldots (3)
20I_2-0.2I_2-4-5(I_2-I_1)=0
5I_1-25.2I_2 = 4 \ldots\ldots (4)
I_1 = -0.05685 A
I_2 = -0.1698 A
I’’_{5 \Omega} = I_2-I_1 = 0.1130 A (\downarrow)
I_{5 \Omega} = I’_{5\Omega} + I’’_{5\Omega} = 0.2288 A (\downarrow)
3) Determine current through 1 \Omega resistor.
Consider a 10 V voltage source only.
-2(I_1-I_2)-2I_1 = 0
-4I_1+2I_2=0 \ldots\ldots (1)
-10 -2(I_2-I_1)-I_2=0
2I_1-3I_2=10 \ldots\ldots (2)
I_1 = -2.5 A
I_2 =-5 A
I’_{1\Omega} = -5 A (\rightarrow)
Consider a 6 V voltage source only.
-2I_1-2(I_1-I_2)-6 = 0
-4I_1+2I_2=6 \ldots\ldots (3)
-I_2+6-2(I_2-I_1)=0
2I_1 – 3I_2 =-6 \ldots\ldots (4)
I_1 = -0.75 A
I_2 =1.5 A
I’’_{1\Omega} = 1.5 A (\rightarrow)
Consider 8 V only.
8-2I_1-2(I_1-I_2)=0
-4I_1+2I_2=-8 \ldots\ldots (5)
-I_2-2(I_2-I_1)=0
2I_1-3I_2=0 \ldots\ldots (6)
I_1 = 3 A
I_2 = 2 A
I’”_{1\Omega} = 2 A (\rightarrow)
Total \; \; current \; \; I_{1 \Omega}=I’_{1 \Omega}+I’’_{1 \Omega}+I’’’_{1 \Omega}
I_{1 \Omega}= 2+1.5+(-5) = -1.5 A (\rightarrow)
I_{1 \Omega} = 1.5 A (\leftarrow)
4) Find current through 20 \Omega resistor.
For Mesh 1:
10-10I_1+10I_2=0
-10I_1+10I_2=-10 \ldots \ldots(1)
For Mesh 2:
-10I_2+10I_1-I_2-20I_2=0
10I_1-31I_2=0 \ldots\ldots(2)
I_1 = 1.4761 A
I_2 = 0.4761 A
I’_{20\Omega} = 0.4761 A (\downarrow)
Consider 8 V voltage source only.
-I-8-20I=0
-21I = 8
I’’_{20\Omega} = -0.3809 A (\downarrow)
Consider a 12 V voltage source only.
-12-8I_1+8I_2=0
-8I_1+8I_2=12 \ldots\ldots(3)
-I_2-8I_2+8I_1-20I_2=0
8I_1-29I_2=0 \ldots\ldots(4)
I_1=-2.0714 A
I_2=-0.5714 A
I’’’_{20\Omega} = -0.5714 (\downarrow)
I_{20\Omega} = I’_{20\Omega}+I’’_{20\Omega}+I’’’_{20\Omega}
I_{20\Omega} = 0.4761+(-0.3809)+(-0.5714)
I_{20\Omega} = -0.4762 A (\downarrow)
I_{20\Omega} = 0.4762 A (\uparrow)
1)A single phase 90 kVA, 3.2 kV/220 V, 50Hz transformer has 89\% efficiency at unity power factor both at full load and half load. Determine the efficiency at 70\% of full load and 0.8 power factor.
\eta_{100\%}=\eta_{50\%}
\dfrac{VIcos\phi}{VIcos\phi+P_i+P_{cu}}=\dfrac{xVIcos\phi}{xVIcos\phi+P_i+x^2P_{cu}}
\dfrac{VIcos\phi}{VIcos\phi+P_i+P_{cu}}=\dfrac{0.5VIcos\phi}{0.5VIcos\phi+P_i+0.5^2P_{cu}}
P_i+(0.5)^2P_{cu}=0.5P_i+0.5P_{cu}
P_i-0.5P_i=0.5P_{cu}-(0.5)^2P_{cu}
P_{cu}=2P_i
Efficiency at 100\%
\eta_{100\%}= \dfrac{VIcos\phi}{VIcos\phi+P_i+P_{cu}}
\eta_{100\%}= \dfrac{VIcos\phi}{VIcos\phi+3P_i}
\eta_{100\%}= \dfrac{90\times 10^3}{90\times 10^3+3P_i}
P_i = 3707.8651 W
P_{cu} =2 P_i = 7415.7302 W
Now efficiency at 70\% of full load
\eta_{70\%} = \dfrac{xVIcos\phi}{xVIcos\phi+P_i+x^2P_{cu}}
\eta_{70\%} = \dfrac{0.7\times 90\times 10^3 \times 0.8}{0.7\times 90\times 10^3 \times 0.8+3707.8651+0.7^2 \times 7415.7302}
\eta_{70\%} = 87.28 \%
1) The plate area of parallel plate capacitor is 0.01 m^2. The distance between the plate is 2.5 cm. The insulating medium is air. Find capacitance, if the space between the plates is filled with an insulating material of relative permittivity 5?
C = \dfrac{\epsilon_0 \epsilon_r A }{d}
C = \dfrac{8.854 \times 10^{-12} \times 1 \times 0.01}{2.5 \times 10^{-1}}
C = 3.5416 \times 10^{-12} F
for \epsilon_r = 5
C = \dfrac{\epsilon_0 \epsilon_r A }{d}
C = \dfrac{8.854 \times 10^{-12} \times 5 \times 0.01}{2.5 \times 10^{-1}}
C = 1.7708 \times 10^{-11}
2) A parallel plate capacitor has a plate area of 500 cm^2 , a plate separation of 0.15 mm and air as a dielectric. Find the capacitance. Also find the voltage between the plates the electric flux density and electric field strength, if the capacitor has a charge of 2 \mu C.
C = \dfrac{\epsilon_0 \epsilon_r A }{d}
C = \dfrac{8.854 \times 10^{-12} \times 1 \times 500 \times 10^{-4}}{0.15 \times 10^{-3}}
C = 2.9513 \times 10^{-9} F
Q = CV
V = \dfrac{Q}{C}
V = \dfrac{2 \times 10^{-6}}{2.9513 \times 10^{-9} }
V = 677.6674 V
D = \dfrac{2 \times 10^{-6}}{500 \times 10^{-4}}
D = 4 \times 10^{-5} \; C/m^2
E = \dfrac{V}{d}
E = \dfrac{677.6674}{0.15 \times 10^{-3}}
E = 4517782.667 V/m
3) Two parallel metal discs, each 100 mm in diameter, are spaced 1 mm apart, the dielectric being air. Calculate the electric field intensity and capacitance.
A = \dfrac{\pi d^2}{4}
A = 0.007854 m^2
E = \dfrac{V}{d} = \dfrac{10^3}{10^{-3}}
E = 10^6
C = \dfrac{\epsilon_0 \epsilon_r A }{d}
C = \dfrac{8.854 \times 10^{-12} \times 1 \times 0.007854}{10^{-3}}
C = 6.9539 \times 10^{-11} F
4) The plate area of a parallel plate capacitor is 0.01 m^2. The distance between the plates is 2.5 cm. The insulating medium is air. Find its capacitance. What would be its capacitance, if the space between the plates is filled with an insulating material of relative permittivity 5?
C = \dfrac{\epsilon_0 \epsilon_r A }{d}
C = \dfrac{8.854 \times 10^{-12} \times 1 \times 0.01}{2.5 \times 10^{-2}}
C = 3.5416 \times 10^{-12} F
For \epsilon_r = 5
C = \dfrac{\epsilon_0 \epsilon_r A }{d}
C = \dfrac{8.854 \times 10^{-12} \times 5 \times 0.01}{2.5 \times 10^{-1}}
C = 1.7708 \times 10^{-11} F
5) A 5 \muF capacitor is charged to a potential difference of 110 V and then connected in parallel with an uncharged 3 \muF capacitor. Calculate the potential difference across the parallel capacitor.
Q_1 = C_1 \times V_1 = 5 \times 10^{-6} \times 110 = 5.5 \times 10^{-4} C
Both the capacitors are connected in parallel. Therefore voltage across both the capacitor will remain same.
V_1 = V_2
\dfrac{q_1}{C_1} = \dfrac{q_2}{C_2}
Now capacitor C_2 is uncharged, therefore the charge will flow from C_1 to C_2 and this flow of charge will stop when the potential difference across C_1 and C_2 will become equal i.e. V_1 = V_2. Capacitor C_1 will loose charge say q_2 and capacitor C_2 will gain that charge q_2. Hence new charge on C_1 will become q_1.
\therefore Charge on C_1 will be q_1 = Q_1 – q_2
\dfrac{Q_1 – q_2}{C_1} = \dfrac{q_2}{C_2}
\dfrac{(5.5 \times 10^{-4}) – q_2}{5 \times 10^-6} = \dfrac{q_2}{3 \times 10^-6}
q_2 = 2.06525 \times 10^{-4}
V_1 = V_2 = \dfrac{q_2}{C_2} = 68.75 V
Method 2
Q_1 = C_1 \times V_1 = 5.5 \times 10^{-4} C
When the capacitors are connected in parallel, the total capacitance is 8 \mu F and the charge of 0.01 C is divided between the two capacitor.
Q = CV
V = \dfrac{Q}{C}
V = \dfrac{5.5 \times 10 ^{-4}}{8 \times 10^{-6}}
V = 68.75 V
6) A 2 \mu F capacitor is charged to 100 V and 3 \mu F capacitor to 200 V. After disconnecting the supply capacitor terminal of similar polarity are connected together calculate the potential difference between the terminal.
Initial charge on each capacitor.
Q_{1i} = C_1V_1 = 2 \times 10^{-6} \times 100 = 2 \times 10^{-4} C
Q_{2i} = C_2V_2 = 3 \times 10^{-6} \times 100 = 6 \times 10^{-4} C
Now, V_1 = V_2
\dfrac{Q_{1i} + Q}{C_1} = \dfrac{Q_{2i} – Q}{C_2}
\dfrac{2 \times 10^{-4} + Q}{ 2 \times 10^{-6}} = \dfrac{6 \times 10^{-4} – Q}{ 3 \times 10^{-6}}
Q = 1.2 \times 10^{-4} C
V_1 = V_2 = \dfrac{Q_{1i} + Q}{C_1} = \dfrac{( 2 \times 10^{-4} )+(1.2 \times 10^{-4})}{ 2 \times 10^{-6} } = 160 \;V
Note: In the above numerical Q_{1i} < Q_{2i}, therefore after connecting similar terminals of the capacitors capacitor C_2 will lose some charge and C_1 will gain some charge
1) A capacitor having capacitance of 4 \mu F is connected in series with a resistance of 1 M\Omega across 200 V DC supply. Find – 1) time constant 2) The initial charging current 3) The time taken by capacitor to raise up to 160 V.
\tau = RC = 1 \times 10^{6} \times 4 \times 10^{6} = 4 sec
I_0 = \dfrac{V}{R} = \dfrac{200}{10^6} = 200 \times 10^{-6} A
V_C = V (1 – e^{\frac{-t}{\tau}})
160 = 200(1-e^{\frac{-t}{4}})
t = 6.4377 sec
Get solved examples on Kirchhoff’s voltage law. We will find current by using KVL in the given circuit. This problem solving technique is also known as Mesh analysis.
1) An iron ring has its mean length of flux path as 60 cm and its cross-sectional area as 15 cm². If relative permeability is 500. Find the current required to be passed through a coil of 300 turns wound uniformly around it to produce a flux density of 1.2 T. What would be the flux density with the same current if the iron ring is replaced by an air core.
Given: l = 60 cm; a = 15 cm²; \mu_r = 500 ; N = 300; B=1.2 T.
MMF(F) = \dfrac{Bl}{\mu_0 \mu_r}
F = \dfrac{1.2 \times 60 \times 10^{-2}}{4\pi \times 10^{-7}\times 500}
F = 1145.9155 AT
If iron ring is replaced by air core.
MMF(F) = \dfrac{B_{air}l}{\mu_0 \mu_r}
B_{air} = 2.4 \times 10^{-3} T
2) A coil of 600 turns and resistance of 10 \Omega is wound uniformly over a steel ring of mean circumference of 30 cm and cross sectional area of 9 cm^2 . It is connected to a supply of 20 V if the relative permeability of the ring is 1600. Find 1) Reluctance 2) Magnetic field intensity 3) MMF 4) Flux.
i) Reluctance:
S = \dfrac{l}{\mu_0 \mu_r a}
S = \dfrac{30 \times 10^{-2}}{4 \times 10^{-7} \times 1600 \times 9 \times 10^{4}}
S = 165786.3991 \; AT/Wb
ii) Magnetic field intensity:
I = \dfrac{V}{R}
I = \dfrac{20}{10}
I = 2 \; A
H = \dfrac{NI}{l}
H = \dfrac{600 \times 2}{30 \times 10^{-2}}
H = 4000 AT/m
iii) MMF = NI = 600 \times 2 = 1200 AT.
iv) Flux:
\phi = \dfrac{600 \times 2}{165786.3991}
\phi = 7.2382 \times 10^{-3} \; Wb
3) A ring shaped core is made up of two parts of the same material. Part one is a magnetic path of length 25 cm and with cross sectional area 4 cm^2, whereas part two is of length 10 cm and cross section area of 6 cm^2. The flux density in part two is 1.5 T. If the current through the coil, wound over core is 0.5 A. Calculate the number of turns of coil. Assume \mu_r for material is 1000.
Given: l_1 = 25 cm; l_2 = 10 cm; a_1 = 4 cm^2; a_2 = 6 cm^2; B = 1.5 T; \mu_r = 1000
S = S_1 + S_2
S = \dfrac{l_1}{\mu_0 \mu_r A_1} + \dfrac{l_2}{\mu_0 \mu_r A_2}
S = \dfrac{1}{4\pi \times 10^{-7} \times{10^3}} \left[ \dfrac{0.25}{4\times 10^{-4}} + \dfrac{0.1}{6\times 10^{-4}} \right]
S = 629988.3164 AT/Wb.
B_2 = \dfrac{\phi}{A_2}
\phi = 1.5 \times 6 \times 10^{-4} = 9 \times 10^{-4} Wb.
F = \phi \times S
NI = \phi \times S
N = \dfrac{S \phi}{I} = \dfrac{629988.3164 \times 9 \times 10^{-4}}{0.5}
N = 1133.98 = 1134 T.
In this tutorial we will solve problems based on inductance of transmission line.
In this HTML tutorial for beginners we will learn what is HTML? and software required for the course. we will also briefly discuss what is live server and why do we need a live server?
